Baseball seam (2018)
Posted: 2019-Mar-03 10:48
What curve is the seam of a baseball or tennis ball? We might be able to find the mathematical solutions on the net. But let's make the curve in "try and error" approach, instead.

The hidden line (curve) should be congruent to the visible line (curve). The shape reminds me of an astroid.
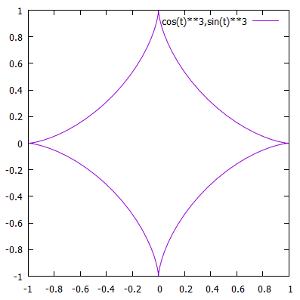
An astroid is a hypocycloid with four cusps, and can be drawn using two circles.
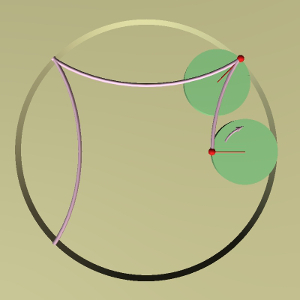
I plotted it on a sphere. It exactly seems to be an astroid in the orthographic xy-plane, but it isn't same with the seam in the ball photo above.
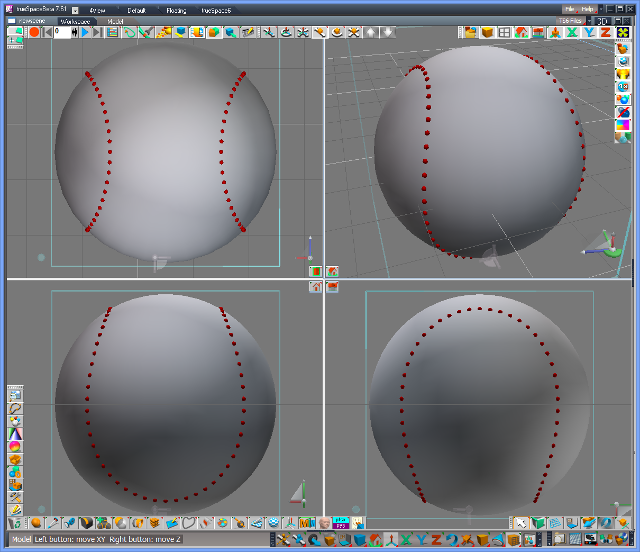
The distance between ")" and "(" must be narrower and the bulge of "U" shape must be larger. In order to get the right distance of ")(", let's draw some curves with different distance changing the cos-component of the astroid (Please read the script for detail).
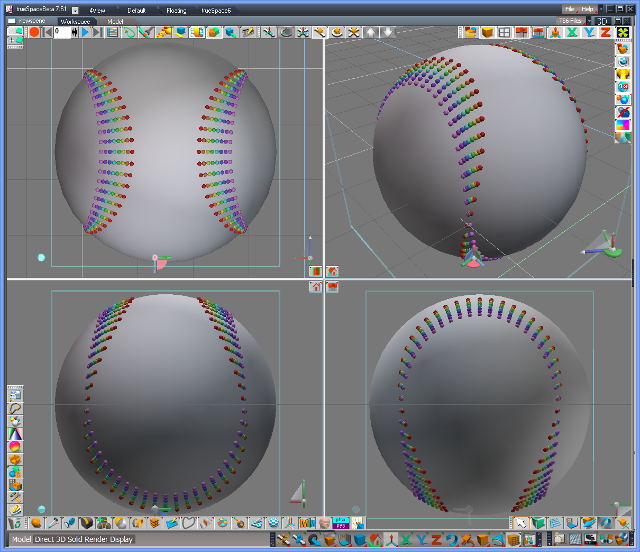

We can now select a "good" distance, but that seems to make the bulge small. Let's fix the distance of the ")(" and draw some curves with different "U" bulges changing the rotation degrees of each points on the curve (Please read the script for detail).
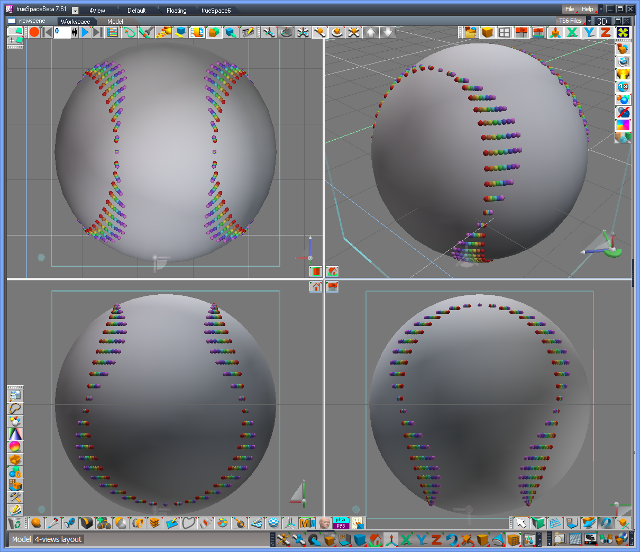
We got an almost good curve.
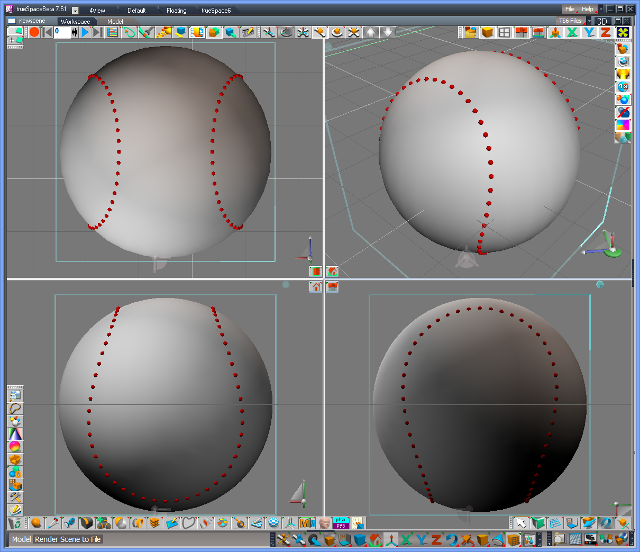
Note: This is not an elegant mathematical approach. This script demonstrates an example of how we can determine the curve of seam with "try and error" (or "cut and try").
Edited on Mar 12 2019:
Updated the attached script file, 3c->3d so that it can be run with ptsxpy 0.0.7.








The hidden line (curve) should be congruent to the visible line (curve). The shape reminds me of an astroid.

An astroid is a hypocycloid with four cusps, and can be drawn using two circles.

I plotted it on a sphere. It exactly seems to be an astroid in the orthographic xy-plane, but it isn't same with the seam in the ball photo above.

The distance between ")" and "(" must be narrower and the bulge of "U" shape must be larger. In order to get the right distance of ")(", let's draw some curves with different distance changing the cos-component of the astroid (Please read the script for detail).


We can now select a "good" distance, but that seems to make the bulge small. Let's fix the distance of the ")(" and draw some curves with different "U" bulges changing the rotation degrees of each points on the curve (Please read the script for detail).

We got an almost good curve.

Note: This is not an elegant mathematical approach. This script demonstrates an example of how we can determine the curve of seam with "try and error" (or "cut and try").
Edited on Mar 12 2019:
Updated the attached script file, 3c->3d so that it can be run with ptsxpy 0.0.7.