Note: Followings are not explanations for any mathematically elegant solution. Our goal here is to find a way to shape the ball anyway.
What approach should we take? A soccer ball is similar to a fullerene (or [latexin]C_{60}[/latexin]), but is not a polyhedron but a ball. Should we do boolean subtract between a sphere and pentagonal/hexagonal pyramids that construct a fullerene? To get the coordinates of the vertices of a fullerene, should we cut all vertices of a regular icosahedron? To do that, should we use a regular dodecahedron as a drill? trueSpace can make a regular icosahedron from its primitive set but cannot easily make a dodecahedron as far as i know. Do we use two cubes to get vertices of a dodecahedron?

Fig. 1
It may be better that we observe the ball well again. A soccer ball has some pentagons and hexagons on its spherical surface, and there is a network of shallow ditch as a gap between them. Let's take this ditch as our starting point to approach.
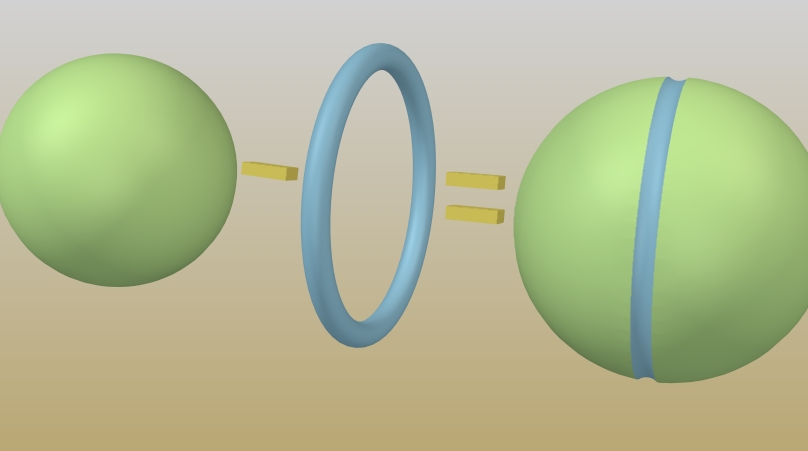
Fig. 2
Bottom of each ditch around the pentagons/hexagons must be a (part of) concentric circle of a great circle because each vertex of the pentagon/hexagon is at equal distances from the center of the sphere.

Fig. 3
In other words, (part of) five tori cut a pentagon on the sphere, the radius of the hole of each torus is slightly small than the radius of the sphere, and the center of the circle (hole) must be same with the center of the sphere. The difference of both radii is the depth of the ditch.
How about the radius of the tube of a torus? How should we determine it? Well, we should be able to determine it by guesswork or trial-and-error because the tube's radius just determines the width and curvature of the ditch.

Fig. 4
If we could determine the angle between an edge and the center of a pentagon, we can rotate a torus and dig a ditch. Of course, the torus must be cut down to a proper length before doing boolean operation with the sphere. The angle to cut the torus must be [latexin]\frac{360}{5}= 72^\circ[/latexin]

Fig. 5

Fig. 6
We can easily dig the first pentagonal ditch on the sphere by rotating the first fragment.

Fig. 7
Let's go back to the rotation angle of a torus in Fig. 4 and try to determine it.
A regular dodecahedron have 12 vertices and their coordonate are:[latex](\pm{1}, \pm{G}, 0)\\(0, \pm{1}, \pm{G})\\(\pm{G}, 0, \pm{1})[/latex]where G is golden ratio:[latex]\begin{eqnarray}
&G =& \frac{1+\sqrt{5}}{2} = 1.6180339887...\\
&G^2 =& \frac{6+2\sqrt{5}}{4} = \frac{3+\sqrt{5}}{2} = 1 + G
\end{eqnarray}[/latex]Proof omitted, but it can be done using Pythagorean theorem.
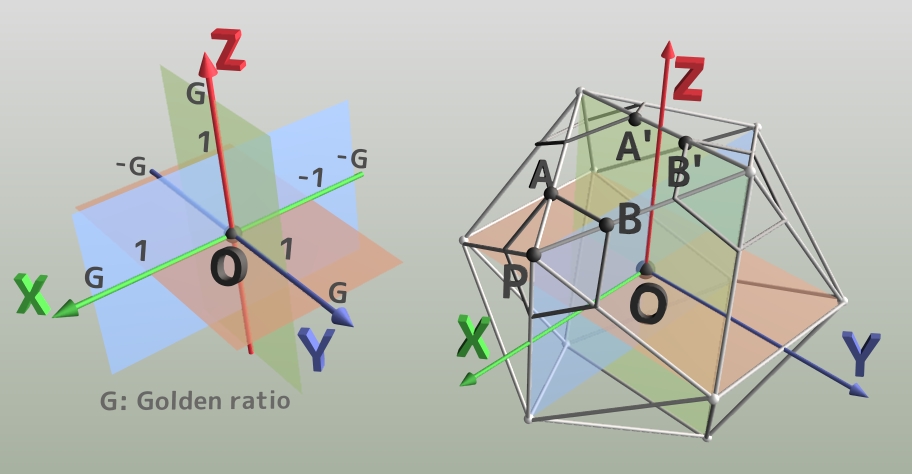
Fig. 8
We give name to some points of a dodecahedron (Fig. 8):
[latexin]P(G,0, 1)[/latexin] : A vertex of the dodecahedron.
[latexin]A, B[/latexin]: two vertice of a pentagon that [latexin]OP[/latexin] crosses the center of it.
[latexin]A', B'[/latexin]: they are on the same plane with [latexin]\triangle [/latexin]PAB, and [latexin]AB \parallel A'B'[/latexin]
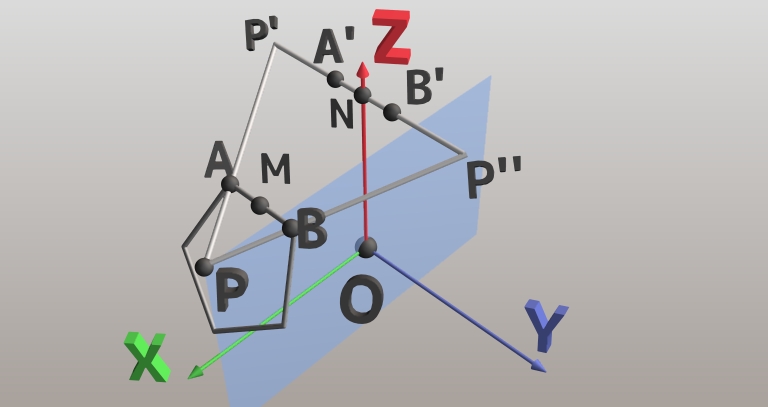
Fig. 9
In Fig. 9, [latexin]M[/latexin] is the midpoint of [latexin]AB[/latexin], [latexin]N[/latexin] is the midpoint of [latexin]A'B'[/latexin]. We add names, [latexin]P'[/latexin] and [latexin]P''[/latexin] to other vertice of the triangle. [latexin]\triangle{PP'P''}[/latexin] is a face of the dodecahedron. The [latexin]P[/latexin], [latexin]M[/latexin], and [latexin]N[/latexin] are on the [latexin]xz[/latexin]-plane. The rotation angle for the torus that we want to know (Fig. 4) is [latexin]\angle{POM}[/latexin]. The angle is difference of other 2 angles:[latex]\angle{POM} = \angle{PON} - \angle{MON}[/latex][latexin]ON[/latexin] is in the [latexin]z[/latexin]-axis, and the coordinate of [latexin]P[/latexin] is [latexin](G,0, 1)[/latexin]. Therefore:[latex]\angle{PON} = \arctan{G}[/latex]
The length of [latexin]ON[/latexin] is [latexin]G[/latexin] (see fig. 8). The length of [latexin]OM[/latexin] is also [latexin]G[/latexin] because both [latexin]AB[/latexin] and [latexin]A'B'[/latexin] are edge of a hexagon and [latexin]OA = OB = OA' = OB'[/latexin]. The length of [latexin]MN[/latexin] is [latexin]\frac{2}{3}PN[/latexin] because [latexin]AB[/latexin] and [latexin]A'B'[/latexin] are edges of a hexagon and [latexin]\frac{PA}{PP'} = \frac{1}{3}[/latexin]. The length of [latexin]NP''[/latexin] is 1.[latex]MN = \frac{2}{3}PN = \frac{2\sqrt{3}}{3}NP'' = \frac{2}{\sqrt{3}}[/latex]Therefore:[latex]\angle{MON} = 2\arcsin({\frac{\frac{MN}{2}}{G}}) = 2\arcsin(\frac{1}{G\sqrt{3}})[/latex]
[latex]\begin{eqnarray}\therefore \angle{POM} &=& \angle{PON} - \angle{MON}\\&=& \arctan{G} - 2\arcsin(\frac{1}{G\sqrt{3}})\end{eqnarray}[/latex]
Again, in this work, the author is not interested in whether the formula is simple or not.
Using these angles, we can make a drill for boolean operation to dig the first pentagonal ditch. Let's rotate the drill or sphere around the normal vector of a pentagon to dig the pentagonal ditch, then, rotate around another pentagon's normal vector, and repeat to dig.

Fig. 10
The remaining work is to dig three edges of each hexagon to connect between each pentagon. Please read the attached sample script for datail. If you want to observe the progress, insert an invalid code like "stop" in any line you want to stop.
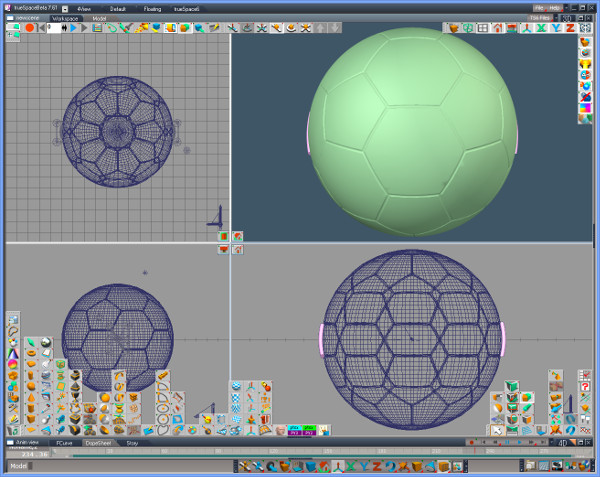
Fig. 11
Please note that the script uses a pair of drill to reduce time (Fig. 11) and it does not use the coordinates in the Fig. 8 and 9 but uses the value of [latexin]\angle{POM}[/latexin] and [latexin]72^\circ[/latexin].
Added on Apr 25 2021:
If you would like to 3D print the ball with color, it would be better to gather several colored objects (pentagonal pyramids, hexagonal pyramids, and padding objects) than this way to approach because it should be hard work to select each (faceted) curved face to paint using the trueSpace.
Edited on Mar 12 2019:
Updated the attached script file, 1_4->1_5 so that it can be run with ptsxpy 0.0.7.
